Processing using Memory

Today we will discuss the concept put forward by an amazing paper titled:

V. Seshadri et al., "Ambit: In-Memory Accelerator for Bulk Bitwise Operations Using Commodity DRAM Technology," 2017 50th Annual IEEE/ACM International Symposium on Microarchitecture (MICRO), 2017
(link opens a new tab with pdf ~ 2.6MB)
IEEE Page (link opens a new tab): https://ieeexplore.ieee.org/document/8686556

This post takes a brief look at the concept however the paper goes in depth reasoning the approach and ways to realize it in commodity hardware. I highly recommend reading the paper if you would like to learn more about the mechanism that enables this compute in DRAM. If you like a higher bandwidth medium like video, you can find the more recent talk by Nastaran Hajinazar about SIMDRAM on Youtube (link opens a new tab) that talks about the entire system right from programming interface and Instruction Set Architecture to realizing the mechanism in hardware in their talk and their paper.

A diagram showing OR operation with Processing in memory where two data rows are opened together with a fully charged compute row to effectively perform an OR operation.

 Alt: A diagram showing OR operation with Processing in memory where two data rows are opened together with a fully charged compute row to effectively perform an OR operation.
The picture is made using https://excalidraw.com/ (link will open a new tab)


DRAM Cell Design

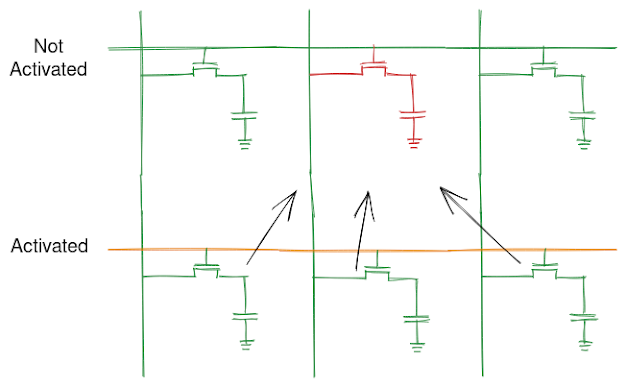
A DRAM cell consists of two parts - a storage capacitor and a transistor. The capacitor stores the charge and transistor guards the access to charge. These cells are arranged in form of an array and the data is accessed using a address line and a bit line - the address line activates a particular row and the bit line carries the charge fro the particular cell it is connected to.

The diagram shows the structure of a DRAM cell with a storage capacitor and a transistor. When the transistor is activated using wordline, the charge from capcitor flows into the bit line and can be stored or read.
Alt: The diagram shows the structure of a DRAM cell with a storage capacitor and a transistor. When the transistor is activated using address line, the charge from capacitor flows into the bit line and can be stored or read.
Source (link opens a new tab): https://electronics.stackexchange.com/questions/306002/why-does-a-dram-cell-necessarily-contain-a-capacitor

The gate connected to the address line restricts the flow of charge from capacitor into bit line. When the transistor is activated via the address line, the charge flows into the bit line and we can see if capacitor is charged signifying 1 or uncharged signifying 0.

The charge dissipates from the capacitor eventually and hence the capacitor is recharged periodically to preserve the correct state. If the level is over half, the capacitor is charged to show 1 and if it is below half, the capacitor is discharged to signify 0.

 

Charges and Equilibrium

When two bodies are connected by a physical medium such as wire and they have a potential difference, the charges from one body to another until a equilibrium is reached.

A depiction of how unbalanced charges reach equilibrium once connected by a wire.

Alt: A depiction of how unbalanced charges reach equilibrium once connected by a wire.
The picture is made using https://excalidraw.com/ (link will open a new tab)

Once reached equilibrium, the charge level remains same between both bodies. If n bodies with charge q and y uncharged bodies are connected to each other, the final equilibrium state will be reached with all bodies with a charge of

q (final) = (n * q) / (n + y)

So if one charged body with charge q is connected to 2 uncharged body, the final equilibrium is reached with each body having a charge = q * (1 / 3)


Computation in DRAM

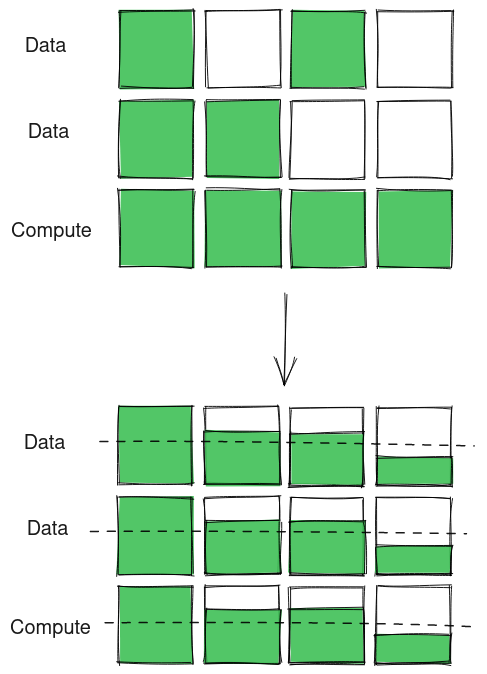
Let us look at the working of Compute DRAM. In Compute DRAM, data to be operated on are brought into data rows. A compute / operation row is pre-charged based on the operation. All rows are opened at once for charges to balance and finally the compute row is recharged to reveal the output of computation.

Consider the following example for bitwise OR:


The diagram above shows Compute DRAM operation for bitwise OR. The data is loaded into data rows and he compute row is precharged. Once opened, the charges balance as follows: for data cells with 1 and 1, the charge equalizes to 1, for data cells with 0 and 1 or 1 and 0, the charges equalizes to 2/3 and for data cells with 0 and 0 the charges equalizes to 1/3. On recharging the compute row, the 1 stays 1, the 2/3 is brought up to 1 and 1/3 is brought down to 0 effectively giving bitwise OR.

Alt: The diagram above shows Compute DRAM operation for bitwise OR. The data is loaded into data rows and he compute row is pre-charged. Once opened, the charges balance as follows: for data cells with 1 and 1, the charge equalizes to 1, for data cells with 0 and 1 or 1 and 0, the charges equalizes to 2/3 and for data cells with 0 and 0 the charges equalizes to 1/3. On recharging the compute row, the 1 stays 1, the 2/3 is brought up to 1 and 1/3 is brought down to 0 effectively giving bitwise OR.
The picture is made using https://excalidraw.com/ (link will open a new tab)

The following example is for bitwise AND:

The diagram above shows Compute DRAM operation for bitwise AND. The data is loaded into data rows and he compute row is uncharged. Once opened, the charges balance as follows: for data cells with 1 and 1, the charge equalizes to 2/3, for data cells with 0 and 1 or 1 and 0, the charges equalizes to 1/3 and for data cells with 0 and 0 the charges equalizes to 0. On recharging the compute row, the 2/3 is brought up to 1, 1/3 is brought down to 0, and 0 stays at 0, effectively giving bitwise AND.
Alt: The diagram above shows Compute DRAM operation for bitwise AND. The data is loaded into data rows and he compute row is uncharged. Once opened, the charges balance as follows: for data cells with 1 and 1, the charge equalizes to 2/3, for data cells with 0 and 1 or 1 and 0, the charges equalizes to 1/3 and for data cells with 0 and 0 the charges equalizes to 0. On recharging the compute row, the 2/3 is brought up to 1, 1/3 is brought down to 0, and 0 stays at 0, effectively giving bitwise AND.
The picture is made using https://excalidraw.com/ (link will open a new tab)

This is how Compute DRAM realize bitwise OR and BITWISE and but the paper goes into details or realizing more complex logic. I highly recommend reading the paper or even watching the video on Computer System for Processing Using Memory by Nastaran Hajinazar linked at the top of this post.

 

Why "Processing using Memory"?

As memory becomes a bottleneck and moving data becomes expensive in terms of energy, paradigms like Processing in Memory and Processing using Memory are gaining popularity among researchers to see whether novel ideas like In DRAM Processing can pave the way forward for a new avenue in computer architecture to extract more performance and influence the design of future general purpose hardware.

Future seems bright for the architects as things are taking hard turn for the better.


Thank you for reading till the end. I'm an undergraduate student keenly interested in Computer Architecture and I look at micro-architectural based attacks to understand more about the working of our hardware. If you find any inaccuracies in the above post, please leave a comment and I'll address it in the next edit. Have a nice day!

Edit: Fixed some typographical errors pointed out by the readers

Comments

Post a Comment

Popular posts from this blog

Prime and Probe

Image
This is the third post in our series of Timing Analysis and I high recommend reading the first two posts - Timing Analysis (link opens a new tab), and Flush and Reload (link opens a new tab). That said if you are aware about cache hierarchy, shared libraries, shared pages, and cache placement policies, you can continue reading this article. In this post we look at Prime and Probe . Alt: An illustration of prime and probe Made with https://excalidraw.com/ (link opens a new tab) Cache Replacement Strategies The placement of data in cache is discussed briefly in Flush and Reload post. Here we will take a look at how data is replaced in cache. There are many different strategies to evict data from cache when a new data is needed to be stored in a filled cache set. Some of them are (some more practical than others): First In First Out (FIFO) - The logic behind the First In First Out is that the data that came first is probably the one that won't be used again for long time and henc
Read more

Row Hammer: Flipping Bits in Memory Without Accessing Them

Image
 This post we'll take a look at Row Hammer, a read disturbance phenomenon observed in commodity DRAM, first unearthed in the paper: Y. Kim et al., "Flipping bits in memory without accessing them: An experimental study of DRAM disturbance errors," 2014 ACM/IEEE 41st International Symposium on Computer Architecture (ISCA '14) (Link opens a new tab with PDF ~ 828KB) IEEE Page (link opens a new tab): https://ieeexplore.ieee.org/document/6853210 In this post I'll only betaking a brief look at the issue and I highly encourage you all to read the paper to find more insights and nitty gritty details of this vulnerability.   Alt: An illustration of Row Hammer showing how an activate of one row can influence the data stored in the adjacent row. The picture is made using https://excalidraw.com/ (link will open a new tab)   Structure of DRAM To fully understand the vulnerability, we must first take a look at the how modern DRAM are structured. All digital data can be represe
Read more

Speculative Execution

Image
 Most of the recent CPU vulnerability discovered depend on the property of modern processors known as Speculative Execution. In this post, we'll take a deeper look at where and why modern processors speculate. Alt: A illustration that shows speculative execution and how the results are committed or discarded based on result of speculation - whether it was correct or not respectively. The picture is made using https://excalidraw.com/ (link will open a new tab) Pipelined Execution Most modern processors are pipelined and are often superscalar in nature running instructions out of order, with multiple stages of execution of instruction running concurrently. Alt: Pipeline of a supersalar processor with 2 instruction fetch every clock cycle and a 5 stage pipeline. Source (link opens a new tab): https://en.wikipedia.org/wiki/Superscalar_processor In case of a long latency cache miss, permission check for an access or conditional branches, the processor generally has to stall waiting for
Read more